CF295D Greg and Caves
首先说一下这题很值得做。
$Update \times n\ on \ 2021.6.30$。
首先题目我们就直接分成两个三角形来写。
之后发现,其实上一行的具体位置不用知道,因为我们枚举当前的长度是必须 $\ge$ 上一次的长度的,然后其所有可能的位置也是很好算的。
我们就开始 $Dp$,设 $f(i,j)$ 表示从上到下计算到第 $i$ 行,当前行的长度 $\le j$ 的方案数。
很显然,我们考虑每一次找一个长度为 $j$ 的方案数。
$$f(i,j) = \sum_{c = 2} ^ m f(i - 1, c) \times (j - c + 1) + 1$$
注意外面的 $ + 1$ 表示在这边重新开一行。
然后我们考虑计算答案,发现直接通过枚举中间的断点然后两个 $f$ 拼起来是错的。因为存在这样的情况。
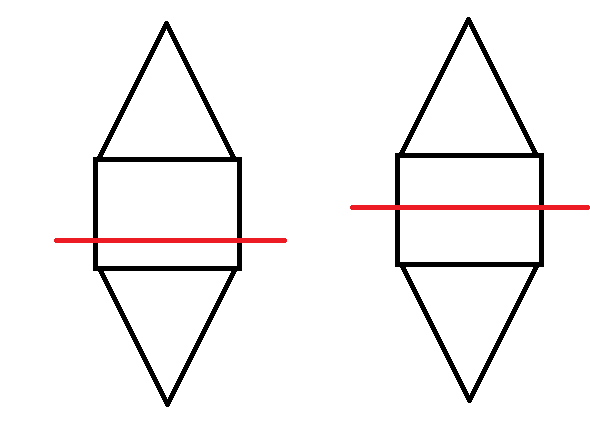
那么我们不妨钦定一下中间这一段的长度,之后让两边严格小于即可,同时保证这个长度为 $1$,方案数就是 $f(i, c) - f(i -1, c)$。
然后我们直接暴力枚举计算即可。
$$
\begin{aligned}
\sum_{i = 1} ^ n \sum_{j = i} ^ n \sum_{k =2} ^ m (dp(i, k) - dp(i - 1, k)) \times (dp(n - j + 1, k) - dp(n - j, k)) \times (m - k + 1) \
\sum_{k = 2} ^ m \sum_{i = 1} ^ n (dp(i, k) - dp(i - 1, k)) \sum_{j = i} ^ n (dp(n - j + 1, k) - dp(n - j, k))\times (m - k + 1) \
\end{aligned}
$$
但是真的只有这样吗?
在更深的理解意义上,我们思考我们的 $f$ 记录了什么东西。就是顶点在 $1 \sim i$ 的所有情况。
那么我们考虑一下为什么要枚举 $j$,而不是直接计算,这其实是为了钦定中间长度为 $k$ 的部分是 $n - i - j$ 这一段。
这边需要更加深刻地理解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
| #include <bits/stdc++.h>
using namespace std;
#define Getmod
#ifdef Fread
char buf[1 << 21], *iS, *iT;
#define gc() (iS == iT ? (iT = (iS = buf) + fread (buf, 1, 1 << 21, stdin), (iS == iT ? EOF : *iS ++)) : *iS ++)
#endif
template <typename T>
void r1(T &x) {
x = 0;
char c(getchar());
int f(1);
for(; c < '0' || c > '9'; c = getchar()) if(c == '-') f = -1;
for(; '0' <= c && c <= '9';c = getchar()) x = (x * 10) + (c ^ 48);
x *= f;
}
#ifdef Getmod
const int hater = 1e9 + 7;
template <int mod>
struct typemod {
int z;
typemod(int a = 0) : z(a) {}
inline int inc(int a,int b) const {return a += b - mod, a + ((a >> 31) & mod);}
inline int dec(int a,int b) const {return a -= b, a + ((a >> 31) & mod);}
inline int mul(int a,int b) const {return 1ll * a * b % mod;}
typemod<mod> operator + (const typemod<mod> &x) const {return typemod(inc(z, x.z));}
typemod<mod> operator - (const typemod<mod> &x) const {return typemod(dec(z, x.z));}
typemod<mod> operator * (const typemod<mod> &x) const {return typemod(mul(z, x.z));}
typemod<mod>& operator += (const typemod<mod> &x) {*this = *this + x; return *this;}
typemod<mod>& operator -= (const typemod<mod> &x) {*this = *this - x; return *this;}
typemod<mod>& operator *= (const typemod<mod> &x) {*this = *this * x; return *this;}
int operator == (const typemod<mod> &x) const {return x.z == z;}
int operator != (const typemod<mod> &x) const {return x.z != z;}
};
typedef typemod<hater> Tm;
#endif
template <typename T,typename... Args> inline void r1(T& t, Args&... args) {
r1(t); r1(args...);
}
const int maxn = 2e3 + 5;
const int maxm = maxn << 1;
int n, m;
Tm f[maxn][maxn], g[maxn][maxn];
signed main() {
int i, j;
r1(n, m);
for(i = 2; i <= m; ++ i) f[1][i] = 1;
for(i = 2; i <= n; ++ i) {
Tm x(0), y(0);
for(j = 2; j <= m; ++ j) {
x += f[i - 1][j];
y += f[i - 1][j] * j;
f[i][j] = x * (j + 1) - y + 1;
}
}
for(int c = 2; c <= m; ++ c) {
for(i = n; i; -- i) {
g[i][c] = g[i + 1][c] + (f[n - i + 1][c] - f[n - i][c]);
}
}
Tm ans(0);
for(int c = 2; c <= m; ++ c) {
for(i = 1; i <= n; ++ i) {
ans += (f[i][c] - f[i - 1][c]) * g[i][c] * (m - c + 1);
}
}
printf("%d\n", ans.z);
return 0;
}
|









![UOJ 269 [清华集训2016] 如何优雅地求和 题解](https://img.xjh.me/random_img.php?type=bg&ctype=nature&return=302&seed=866895879)

![P4548 [CTSC2006]歌唱王国](https://img.xjh.me/random_img.php?type=bg&ctype=nature&return=302&seed=756179924)