I. 分组作业

时间限制： 1.0 秒

空间限制： 512 MiB

相关文件： 题目目录

题目描述

老师布置了分组作业。在此之前，老师将班上 $2n$ 个学生分成了 $n$ 组，每组两个人。其中 $1$ 号和 $2$ 号为一组，$3$ 号和 $4$ 号为一组，……，$2n-1$ 号和 $2n$ 号为一组。

老师让每个队伍自行安排分工。这样是否合作就成了一个大问题。大家决定用表决的方式来确定。首先每个人决定是否愿意和队友合作。不同的人因为自己的原因和分配的队友的原因，对合作的意愿不一样，对于第 $i$ 个学生，选择“愿意”会产生 $c_i$ 的不满，选择“不愿意”会产生 $d_i$ 的不满。

如果两名队友都选择“愿意”，那么根据实际情况他们可以合作或者不合作。但是如果有一名队友选择“不愿意”，那么他们只能不合作。

学生中还有 $m$ 个单向的喜欢关系，一个关系形如“$A$ 喜欢 $B$”。在这样一个关系中，如果 $A$ 没有和队友合作，且 $B$ 选择了“愿意”，$A$ 会有略微沮丧，产生 $a_i$ 的不满；如果 $A$ 表决了“不愿意”，但 $B$ 成功与队友合作，那么 $A$ 会羡慕嫉妒恨并产生 $b_i$ 的不满。（由于当 $A$ 和 $B$ 在同一组时这种设定会变得很奇怪，所以题目保证不会有这种情况）其中 $i$ 表示第 $i$ 个关系。

如果一个学生 $i$ 选择了“愿意”但是他的队友选择了“不愿意”，那么他会因为队友产生 $e_i$ 的不满。

问所有情况下最小的不满之和是多少。

输入格式

从标准输入读入数据。

第一行两个整数 $n,m$。

接下来 $2n$ 行，每行三个整数 $c_i,d_i,e_i$。

接下来 $m$ 行，每行四个正整数 $A,B,a_i,b_i$ 。

输出格式

输出到标准输出。

一行一个整数表示答案。

样例输入

1
2
3
4
5
6
2 1
8 6 7
5 2 8
7 1 5
6 5 8
1 4 4 3

样例输出

1
14

子任务

保证 $1\le n \le 5000$，$0\le m \le 10000$，$1\le a_i,b_i,c_i,d_i,e_i\le 10^9$。时间限制： 1.0 秒

空间限制： 512 MiB

相关文件： 题目目录

题目描述

老师布置了分组作业。在此之前，老师将班上 $2n$ 个学生分成了 $n$ 组，每组两个人。其中 $1$ 号和 $2$ 号为一组，$3$ 号和 $4$ 号为一组，……，$2n-1$ 号和 $2n$ 号为一组。

老师让每个队伍自行安排分工。这样是否合作就成了一个大问题。大家决定用表决的方式来确定。首先每个人决定是否愿意和队友合作。不同的人因为自己的原因和分配的队友的原因，对合作的意愿不一样，对于第 $i$ 个学生，选择“愿意”会产生 $c_i$ 的不满，选择“不愿意”会产生 $d_i$ 的不满。

如果两名队友都选择“愿意”，那么根据实际情况他们可以合作或者不合作。但是如果有一名队友选择“不愿意”，那么他们只能不合作。

学生中还有 $m$ 个单向的喜欢关系，一个关系形如“$A$ 喜欢 $B$”。在这样一个关系中，如果 $A$ 没有和队友合作，且 $B$ 选择了“愿意”，$A$ 会有略微沮丧，产生 $a_i$ 的不满；如果 $A$ 表决了“不愿意”，但 $B$ 成功与队友合作，那么 $A$ 会羡慕嫉妒恨并产生 $b_i$ 的不满。（由于当 $A$ 和 $B$ 在同一组时这种设定会变得很奇怪，所以题目保证不会有这种情况）其中 $i$ 表示第 $i$ 个关系。

如果一个学生 $i$ 选择了“愿意”但是他的队友选择了“不愿意”，那么他会因为队友产生 $e_i$ 的不满。

问所有情况下最小的不满之和是多少。

输入格式

从标准输入读入数据。

第一行两个整数 $n,m$。

接下来 $2n$ 行，每行三个整数 $c_i,d_i,e_i$。

接下来 $m$ 行，每行四个正整数 $A,B,a_i,b_i$ 。

输出格式

输出到标准输出。

一行一个整数表示答案。

样例输入

1
2
3
4
5
6
2 1
8 6 7
5 2 8
7 1 5
6 5 8
1 4 4 3

样例输出

1
14

子任务

保证 $1\le n \le 5000$，$0\le m \le 10000$，$1\le a_i,b_i,c_i,d_i,e_i\le 10^9$。

发现有很多个限制分别会有影响，像一个最小割模型，我们考虑构造最小割。

考虑对每一个对点进行建图，不妨设其为 $(x, y)$ 然后源点汇点分别为 $S, T$。

不妨考虑设与 $S$ 连边表示不合作，与 $T$ 连边表示合作。

但是我们发现合作的条件是两个点都要同意，所以我们需要额外增加一个点并且让 $x, y$ 连接该点表示是否愿意，与最后的点相连表示合作。

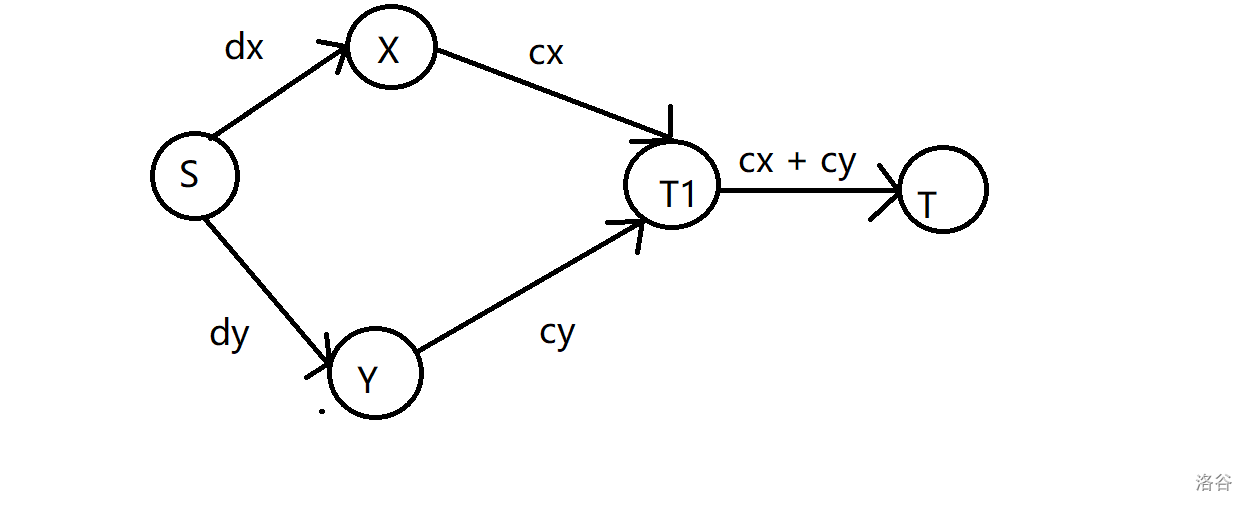
我们还需要考虑如果一个学生 $i$ 选择了“愿意”但是他的队友选择了“不愿意”，那么他会因为队友产生 $e_i$ 的不满。

直接让 $x \to y$ 边权为 $e_i$ 即可。

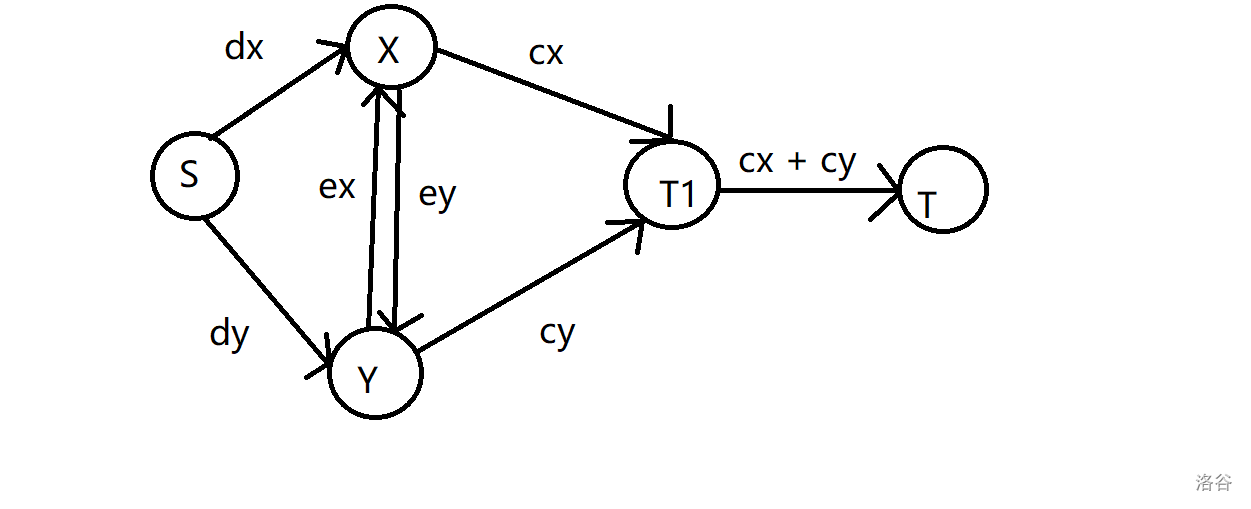
我们接着考虑若干喜欢的关系：

  • 一个关系形如“A 喜欢 B”。在这样一个关系中，如果 A 没有和队友合作，且 B 选择了“愿意”，A 会有略微沮丧，产生 ai 的不满。

也就是意味着 $A$ 选择了不愿意，$B$ 选择了愿意这里需要产生一条 $S \to T$ 的路，我们让 $B \to A$，让边权变成 $a_i$ 即可。

  • 如果 A​​ 表决了“不愿意”，但 B 成功与队友合作，那么 A 会羡慕嫉妒恨并产生 bi 的不满。

可以让 $BT_1 \to A$ 边权为 $b_i$ 即可。